Math : Diffusion Equation or Heat Equation

Diffusion equation at finite rod, Semi-infinite rod and infinite rod have been discussed.

Thank you. Feel free to comment.

Tech : Some Information about Payment Banks in India. What is Payment Banks and it's function?

Payments Banks:

                            This is a new model of bank in India incited by former RBI (Reserve bank of India ) governor Raghuram Rajan (2013-2016) in 2014.

These banks can accept a deposit upto  ₹100,000 ($ 1500 around) per customer.

They can't issue loans and credit cards but can operate savings and current  accounts.  Also they can give services like ATM Cards, Debit Cards,  Online Banking,  Mobile Banking,  UPI Banking  ( Unified Payment Interface,  This service launched by RBI), Aadhaar Banking  (banking system use biometric authentication for payment no need any password or pin)

Requirement for Payments Banks :

                                                           The minimum capital requirement is  ₹100 crore ($ 15m).         Foreign share holding will be allowed in these banks as per rules of FDI ( foreign direct investment ) in the private banks in India.

These banks must use "Payments bank " term in their name. 70% of its deposited amount should be invest in the government bond ( India ) and 25% of its branches must be in the unbanked rural area.

Launched  Payments banks :

                                            Currently "Airtel Payments bank " has been launched on 15th January 2017, India Post has been launched on 30th january 2017 and "Paytm Payments bank" will be launched on the 1st week of February 2017.

RBI already given to these companies to launch Payments bank

1.India Post

  2.Airtel M commerce

3. Airtel M commerce Services

4. Cholamandalam Distribution Services

5. Fino Pay Tech

6. National securities Depository

7. Reliance  Industries

8. Sun pharmaceuticals

9. Paytm

10. Tech Mahindra

11. Vodafone  M pesa   etc.
Thank you.  Come again. Feel free to comment.

Mathematics Syllabus for competitive exams and gate

Section  1:  Linear Algebra

  Finite dimensional  vector  spaces;  Linear  transformations  and  their  matrix representations, rank;  systems  of  linear  equations,  eigenvalues  and  eigenvectors,  minimal  polynomial, Cayley-Hamilton  Theorem,  diagonalization,  Jordan-canonical  form,  Hermitian,  SkewHermitian  and  unitary  matrices;  Finite dimensional  inner  product  spaces,  Gram-Schmidt orthonormalization  process,  self-adjoint  operators,  definite forms.

Section 2: Complex Analysis 

Analytic  functions,  conformal  mappings,  bilinear  transformations;  complex  integration: Cauchy’s  integral  theorem  and  formula;  Liouville’s  theorem,  maximum  modulus  principle; Zeros  and  singularities;  Taylor  and  Laurent’s  series;  residue theorem  and  applications  for evaluating  real  integrals.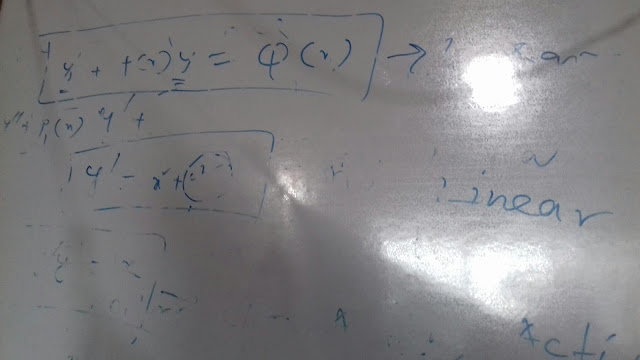

Section 3: Real Analysis 
   Sequences  and  series  of  functions,  uniform  convergence,  power  series,  Fourier  series, functions  of  several  variables,  maxima,  minima;  Riemann integration,  multiple integrals, line,  surface and  volume  integrals,  theorems  of  Green,  Stokes  and  Gauss;  metric  spaces, compactness,  completeness,  Weierstrass  approximation  theorem;  Lebesgue measure, measurable functions;  Lebesgue integral,  Fatou’s  lemma,  dominated  convergence theorem.

Section  4: Ordinary  Differential  Equations 

First  order  ordinary  differential  equations,  existence and  uniqueness  theorems  for  initial value  problems,  systems  of  linear  first  order  ordinary  differential  equations,  linear  ordinary differential  equations  of  higher  order  with constant  coefficients;  linear  second  order ordinary  differential  equations  with variable coefficients;  method  of  Laplace transforms  for solving  ordinary  differential  equations,  series  solutions  (power  series,  Frobenius  method); Legendre and  Bessel functions  and  their  orthogonal  properties.

Section  5:  Algebra

Groups,  subgroups,  normal  subgroups,  quotient  groups  and  homomorphism  theorems, automorphisms;   cyclic  groups  and  permutation  groups,  Sylow’s  theorems  and  their applications;   Rings,  ideals,  prime and  maximal  ideals,  quotient  rings,  unique factorization domains,  Principle ideal  domains,  Euclidean domains,  polynomial  rings  and  irreducibility criteria;  Fields,  finite fields,  field  extensions.

Section  6: Functional  Analysis

  Normed  linear  spaces,  Banach  spaces,  Hahn-Banach  extension theorem,  open mapping and  closed  graph  theorems,  principle  of  uniform  boundedness;  Inner-product  spaces, Hilbert  spaces,  orthonormal  bases,  Riesz  representation  theorem,  bounded  linear operators.

Section  7:  Numerical Analysis  Numerical  solution  of  algebraic  and  transcendental  equations:  bisection,  secant  method, Newton-Raphson method,  fixed  point  iteration;  interpolation:  error  of  polynomial interpolation,  Lagrange,  Newton interpolations;  numerical  differentiation;  numerical integration:  Trapezoidal  and  Simpson  rules;  numerical  solution  of  systems  of  linear equations:  direct  methods  (Gauss  elimination,  LU  decomposition);  iterative  methods :Jacobi  and  Gauss-Seidel);  numerical  solution of  ordinary  differential  equations:  initial value problems:  Euler’s  method,  Runge-Kutta  methods  of  order  2.

Section  8:  Partial  Differential  Equations

Linear  and  quasilinear  first  order  partial  differential  equations,  method  of  characteristics; second  order  linear  equations  in  two  variables  and  their  classification;  Cauchy,  Dirichlet and  Neumann problems;  solutions  of  Laplace,  wave in  two  dimensional  Cartesian coordinates,  Interior  and  exterior  Dirichlet  problems  in polar  coordinates;  Separation of variables  method  for  solving  wave and  diffusion equations  in one space  variable;  Fourier series  and  Fourier  transform  and  Laplace  transform  methods  of  solutions  for  the  above equations.

Section  9: Topology

Basic  concepts of  topology,  bases,  subbases,  subspace  topology,  order  topology, product  topology,  connectedness,  compactness,  countability  and  separation axioms, Urysohn’s Lemma.

Section  10: Probability  and  Statistics Probability  space,  conditional  probability,  Bayes  theorem,  independence,  Random variables,  joint  and  conditional  distributions,  standard  probability  distributions  and  their properties  (Discrete  uniform,  Binomial,  Poisson,  Geometric,  Negative binomial,  Normal, Exponential,  Gamma,  Continuous  uniform,  Bivariate normal,  Multinomial),  expectation, conditional  expectation,  moments;  Weak  and  strong  law  of  large numbers,  central  limit theorem;  Sampling  distributions,  UMVU  estimators,  maximum  likelihood  estimators;  Interval estimation;  Testing  of  hypotheses,  standard  parametric  tests  based  on  normal, , ,    distributions;  Simple  linear  regression.

 Section  11:  Linear  programming

Linear  programming  problem  and  its  formulation,  convex  sets  and  their  properties, graphical  method,  basic  feasible solution,  simplex  method,  big-M  and  two  phase methods;  infeasible  and  unbounded  LPP’s,  alternate optima;  Dual  problem  and  duality theorems,  dual  simplex method  and  its  application in post  optimality  analysis;  Balanced and  unbalanced  transportation problems,  Vogel’s  approximation method  for  solving transportation problems;  Hungarian method  for  solving  assignment  problems. 

Thank you.                                               https://amathscholar.blogspot.in/

SPIRITUAL : SILENCE IS THE MOST POWERFUL WORD IN WORLD

What is the powerful things in the world ?
money? people? No.
#Silence as It has no boundary. So don't think about people or money just about your love and passion. People and money can't give you peace but you can give it to you. It is not matter what people say about you. It is matter what you say about yourself and think about yourself.
You see people are selling each other because other are doing so.
Do you want to be like that people then you can do what they are doing. But if you don't want that do what you think and like.
some people may have bound to do this thing but why should you come in this bound? why would you see world by the other people mirror but your own mirror. ...  It isn't that physical work is so much effective but #Silence . 
Do you have seen Silence sea? Do you know how dangerous is a silence sea? You can't judge anything by seen a silence sea.   If your mind go to the silence position think what mind can do.Is anything impossible for this mind? Silence can can create infinite possibility in the mind. Silence is the more effective than anything in the leaving creature.  
What is the difference between men and other animals? Nothing but Silence. For this men are unstoppable.

Thank you. Come again. Please feel free to comment.

Spritual: Some times I become Thoughtless

Sometimes I become thoughtless and speechless, ask myself what do you want? My mind says don't know. Everything is within me so I don't need anything. Then I ask why are you searching here and there? In reply it says that to increase the awareness that Everything is within me. So why are you frustrated and fear about your job or work? Your job and work can't give anything to you except you. So don't fear do what you want.
Don't greed about anything as you can't get anything. You get what you are. So do what you love and what you think. Never mind what people say or think about you. You came in this world to search your love. For searching love don't afraid about physical pain of your body. In the physical pain of your body you will have your freedom and freedom  is the ultimate goal of your life. Anything isn't matter to you expect freedom. In love there may be physical pain but don't give up your love. In the World you come here to search your love. See everything but choose what you love. Think about the people whom love you most. Do the work what you love.
Don't fear to lose. You are doing what you  love. Don't think about result of the work as you are doing what you love.

Thank you.  Please feel free to  comment.

Tech : BHIM App lunched by Narendra Modi, Best UPI App Review

1 #BHiM  app is one the best upi app. It also very fast and transaction time is less than one sec. 9/10

2 Lotza by Federal bank
Lotza is also very fast app also another feature of this app you can use many upi address and many account at a time. 9/10

3 Sbi pay this app is very very slow. If you wrongly enter your mobile number you can't change it by again uninstaling it.
3/10

4 Axis pay this is axis bank upi app. this app is also not so bad. Some people are facing problem that scan option is not working on their phone. This is not as so fast as first two app. 6/10

5 PhonePe this upi app is also good but one main concern is that you can't transfer your money from phonepe to another upi app. Transaction failure rate is very much. 8/10.

6 other upi app are #pockets and hdfc  upi  etc . they also good

. 

Thank you. Come again. Please feel free to comment. 

Math : Csir Ugc Net syllabus for Mathematics

CSIR-UGC National  Eligibility  Test (NET) for  Junior Research Fellowship and  Lecturer-ship   COMMON SYLLABUS FOR PART ‘B’ AND ‘C’   MATHEMATICAL SCIENCES   

UNIT  –  1

     Analysis:          Elementary  set  theory,  finite,  countable  and uncountable  sets, Real  number system  as  a complete  ordered field, Archimedean property, supremum, infimum.     Sequences  and series,  convergence, limsup,  liminf.     Bolzano Weierstrass  theorem, Heine  Borel  theorem.     Continuity, uniform  continuity, differentiability, mean value  theorem.     Sequences  and series  of  functions, uniform  convergence.     Riemann sums  and Riemann integral, Improper Integrals.     Monotonic  functions, types  of  discontinuity, functions  of  bounded variation, Lebesgue  measure, Lebesgue  integral.     Functions  of  several  variables, directional  derivative, partial  derivative, derivative  as  a  linear transformation, inverse  and implicit  function theorems.     Metric  spaces, compactness, connectedness. Normed linear Spaces. Spaces  of  continuous  functions as  examples.    

 Linear  Algebra:         Vector  spaces, subspaces, linear dependence, basis, dimension, algebra  of  linear transformations.     Algebra  of  matrices, rank  and determinant  of  matrices, linear  equations.     Eigenvalues  and  eigenvectors, Cayley-Hamilton theorem.     Matrix representation of  linear transformations. Change  of  basis, canonical  forms, diagonal  forms, triangular forms,  Jordan forms.     Inner product  spaces, orthonormal  basis.     Quadratic  forms, reduction and classification of  quadratic  forms   

  UNIT  –  2     

Complex  Analysis:  Algebra  of  complex numbers, the  complex plane, polynomials, power series, transcendental  functions  such as  exponential, trigonometric  and hyperbolic  functions.     Analytic  functions, Cauchy-Riemann  equations. Contour  integral, Cauchy’s  theorem, Cauchy’s  integral  formula, Liouville’s  theorem, Maximum modulus  principle, Schwarz  lemma, Open  mapping  theorem.     Taylor series, Laurent  series, calculus  of  residues.     Conformal  mappings, Mobius  transformations.  

   Algebra:  Permutations, combinations, pigeon-hole  principle,  inclusion-exclusion principle, derangements.     Fundamental  theorem  of  arithmetic, divisibility  in  Z,  congruences, Chinese  Remainder Theorem, Euler’s  Ø-  function, primitive  roots.     Groups, subgroups, normal  subgroups, quotient  groups, homomorphisms, cyclic  groups, permutation groups, Cayley’s  theorem,  class  equations, Sylow  theorems.     Rings, ideals, prime  and  maximal  ideals, quotient  rings, unique  factorization  domain, principal  ideal domain, Euclidean  domain.     Polynomial  rings  and irreducibility  criteria.     Fields, finite  fields, field  extensions, Galois  Theory.     

Topology:  basis, dense  sets, subspace  and  product  topology, separation  axioms, connectedness  and compactness. 

    UNIT  –  3    

 Ordinary Differential  Equations  (ODEs):     Existence  and uniqueness  of  solutions  of  initial  value  problems  for first  order  ordinary  differential equations, singular solutions  of  first  order ODEs, system  of  first  order ODEs.     General  theory  of  homogenous  and non-homogeneous  linear ODEs, variation  of  parameters, Sturm-Liouville  boundary  value  problem, Green’s  function.   

  Partial  Differential  Equations  (PDEs):     Lagrange  and Charpit  methods  for solving  first  order PDEs, Cauchy  problem  for first  order PDEs.     Classification of  second order PDEs,  General  solution of  higher order PDEs  with constant coefficients, Method of  separation of  variables  for  Laplace, Heat  and Wave  equations.    

 Numerical  Analysis  :     Numerical  solutions  of  algebraic  equations, Method  of  iteration and Newton-Raphson method, Rate of  convergence, Solution  of  systems  of  linear algebraic  equations  using  Gauss  elimination  and Gauss-Seidel  methods, Finite  differences, Lagrange, Hermite  and spline  interpolation, Numerical differentiation and  integration, Numerical  solutions  of  ODEs  using  Picard, Euler, modified Euler  and    Runge-Kutta  methods.     

Calculus  of  Variations:     Variation of  a  functional,  Euler-Lagrange  equation,  Necessary  and sufficient  conditions  for extrema. Variational  methods  for boundary  value  problems  in ordinary  and partial  differential  equations. 

    Linear  Integral  Equations:     Linear integral  equation of  the  first  and second kind  of  Fredholm  and Volterra  type, Solutions  with separable  kernels. Characteristic  numbers  and  eigenfunctions, resolvent  kernel.  

   Classical  Mechanics:     Generalized  coordinates, Lagrange’s  equations, Hamilton’s  canonical  equations, Hamilton’s principle  and principle  of  least  action, Two-dimensional  motion  of  rigid bodies, Euler’s  dynamical equations  for the  motion  of  a  rigid body  about  an axis, theory  of  small  oscillations.  

   UNIT  –  4    

 Descriptive statistics, exploratory  data analysis     Sample space, discrete probability, independent  events,  Bayes  theorem. Random  variables  and distribution  functions  (univariate  and multivariate);  expectation and moments. Independent  random variables, marginal  and  conditional  distributions. Characteristic  functions. Probability  inequalities (Tchebyshef,  Markov, Jensen).  Modes of  convergence,  weak  and strong  laws  of  large numbers, Central Limit  theorems (i.i.d.  case).     Markov  chains with finite  and countable state  space, classification  of  states, limiting  behaviour  of  n-step transition probabilities, stationary  distribution, Poisson  and birth-and-death processes.     Standard discrete  and continuous univariate distributions. sampling  distributions,  standard  errors and asymptotic distributions,  distribution of  order  statistics  and range.     Methods of  estimation, properties of  estimators, confidence  intervals.  Tests of  hypotheses:  most  powerful and uniformly  most  powerful  tests, likelihood  ratio  tests. Analysis of  discrete  data  and chi-square  test  of goodness  of  fit. Large sample tests.     Simple nonparametric  tests  for  one and two  sample problems, rank  correlation  and  test  for  independence. Elementary  Bayesian inference.  

   Gauss-Markov  models, estimability  of  parameters, best  linear  unbiased estimators,  confidence  intervals, tests  for  linear  hypotheses.  Analysis of  variance and  covariance. Fixed,  random  and mixed effects models. Simple and multiple  linear  regression. Elementary  regression diagnostics.  Logistic  regression.     Multivariate normal  distribution, Wishart  distribution  and their  properties. Distribution of  quadratic forms. Inference  for  parameters, partial  and multiple  correlation coefficients  and related  tests. Data reduction techniques:  Principle component  analysis, Discriminant  analysis, Cluster  analysis, Canonical correlation.   Simple random  sampling, stratified sampling  and systematic sampling. Probability  proportional  to size sampling. Ratio  and  regression methods.     Completely  randomized designs, randomized block  designs and Latin-square designs. Connectedness  and orthogonality  of  block  designs, BIBD. 2K  factorial  experiments:  confounding  and  construction.     Hazard function and failure  rates,  censoring  and life  testing, series and parallel  systems.     

Linear  programming  problem, simplex methods, duality. Elementary  queuing  and  inventory  models. Steady-state solutions of  Markovian queuing  models:  M/M/1,  M/M/1 with limited waiting  space, M/M/C, M/M/C  with  limited waiting  space, M/G/1.  

   All  students  are expected  to  answer  questions from  Unit  I.  Students in  mathematics are expected  to  answer additional  question  from  Unit  II  and  III.    Students  with statistics  are expected  to  answer  additional  question  from  Unit  IV. 

Thank you. Come again . Please feel free to comment.